手把手算电流输出型DAC的IV转换电路原件参数计算及耳机放大器原件参数(参考TI,以ES9038q2m为例)
在使用电流输出型DAC时,我们往往需要作I/V转换,输出电压信号供我们使用,中间牵涉的参数计算有时令人头大。今天,社区用户UM4I为我们带来手把手的保姆级教学。
根据TI手册,我们大概需要这样一个结构。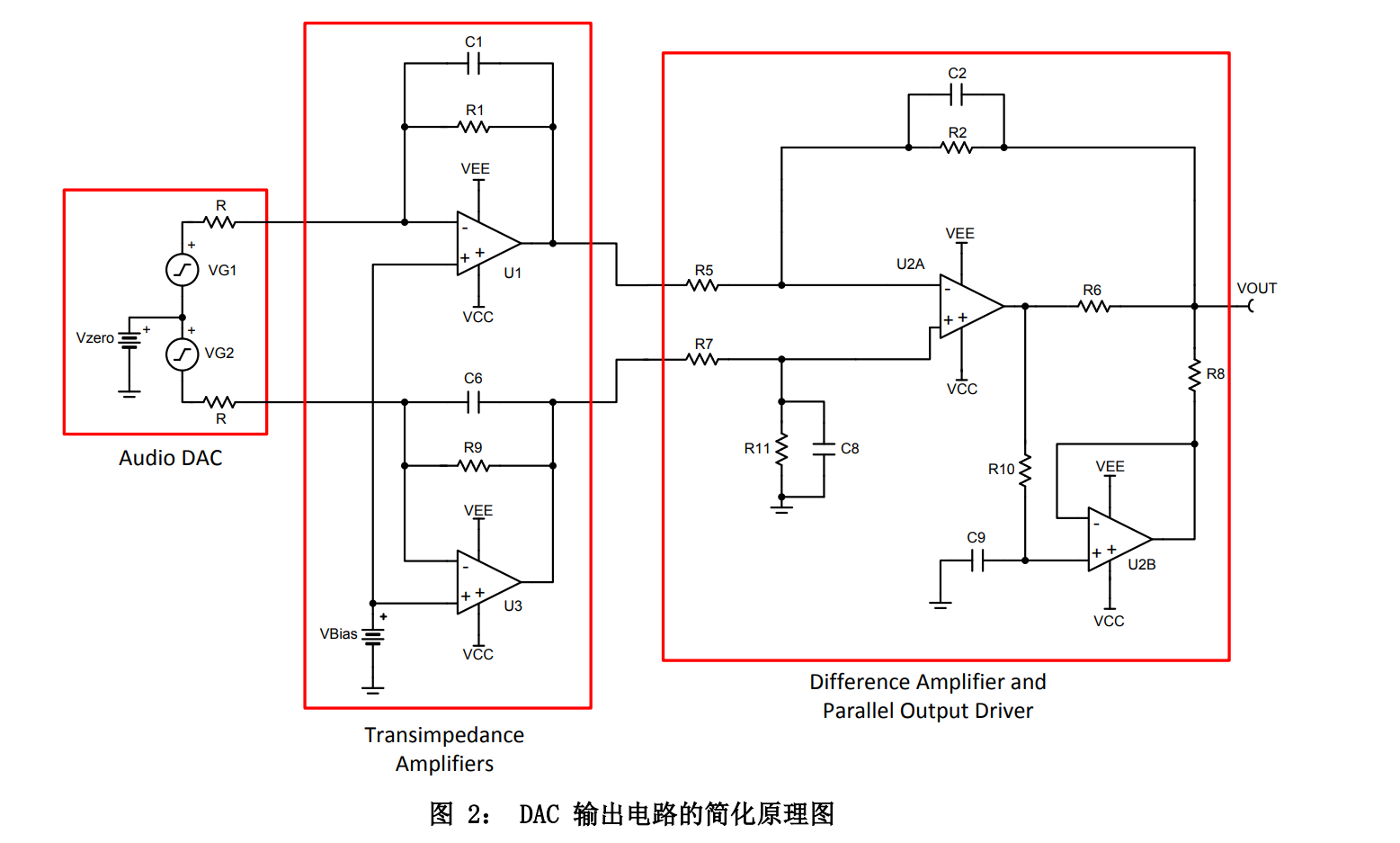
但是IV转换电路的电容C1,C6,电阻R1,R9,偏置电压VBias需要计算。
耳机放大器的电容C8,C2,C9,电阻R5,R7,R2,R11,R10,R6,R8需要计算。
运放需要确定型号。
ti那个文档(参考)很详细,但是有点迷,有的地方有引用前面的数据却没有标识,就写了这个文档手把手算。
本文没写的东西可以参考最下面的参考文档(很详细)。
本文介绍如何计算这些器件的参数。
第一步:计算DAC输出电流
根据dac的数据手册,可以找到类似这样的信息:写明了dac的输出阻抗,电压模式输出范围,电压偏置,电流模式输出范围,及电流模式偏置。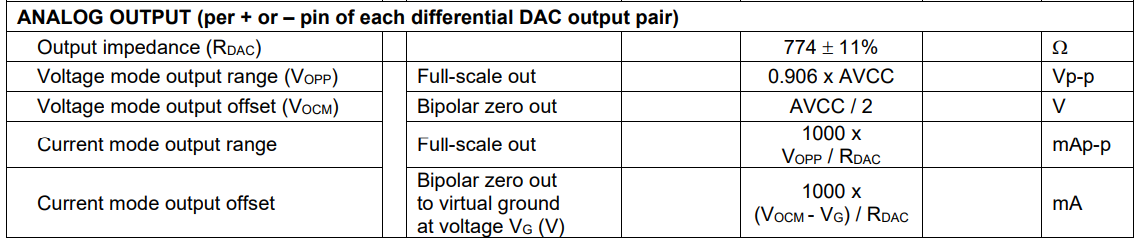
如图,我们需要计算的是电流模式输出范围(也就是最大能输出多少电流,即峰值电流)
计算方法为:
$$
CurrentModeOutputRange=(1000*\frac{V_{opp}}{R_{dac}})mApp
$$
由手册可得,这个dac的内阻是774R,即。
$$
R_{dac}=774_{ohm}
$$
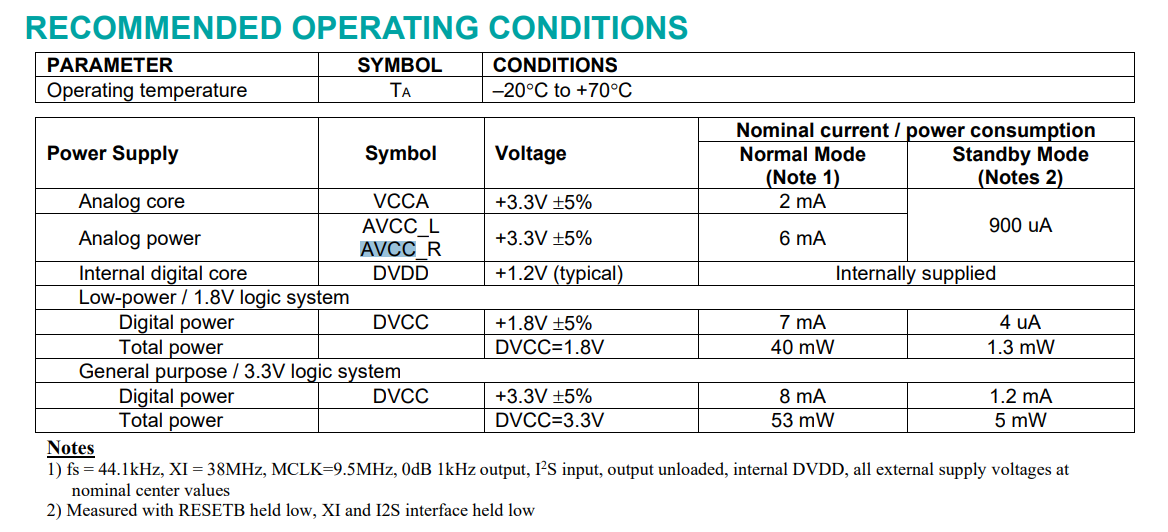
又由手册,Vopp等于0.906* AVCC。
又由手册,AVCC的推荐电压是3.3v,我们在设计中也将采用3.3v这个电压,所以,可得:
$$
AVCC=3.3V
$$
$$
V_{opp}=0.906*AVCC=0.906*3.3=2.9898V
$$
$$
CurrentModeOutputRange=(1000*\frac{V_{opp}}{R_{dac}})=(1000*\frac{2.9898}{774})\approx 3.86279mApp
$$
即dac的正输出(DACxOUT)对负输出(DACxOUTB)能输出的最大电流为正负3.86279mA。
正输出(DACxOUT)或负输出(DACxOUTB)对DAC的参考点(一般电压是AVCC/2)能输出的最大电流为
$$
\frac{CurrentModeOutputRange}{2}=\frac{3.86279}{2}\approx 1.93139mA
$$
后续计算中,大部分使用1.93139mA。
第二步:确定IV转换输出的电压幅度
一般情况下,电压衰减由后续的耳机放大器进行,所以在IV转换时,倾向于设计使其输出达到当前电源轨下运放的最大输出(最大摆幅),来获得更大的信噪比。
最大摆幅在运算放大器数据表中通常作为开环增益测量条件给出。
以opa2188为例:
最大摆幅是(V-)+500mV到(V+)-500mV。
那么,输出的电压幅度也为(V-)+500mV到(V+)-500mV。
第三步:计算IV转换电路的反馈电阻(R1,R9)
在设计中,我们的运放供电V+为5V,V-为-5V。
那么反馈电阻的计算方法为:
$$
R_{fb}=\frac{Voutmax}{Iin}=\frac{5V-0.5V}{1.93139mA}\approx 2.329928Kohm
$$
随后,找到阻值最近的而且能买到的电阻就行了。
在这个设计里面选择2.26Kohm电阻。
根据这个电阻值反推出来的单端(正输出或负输出对地)电压输出峰值的绝对值为:
$$
v_{out}=R_f * I_{in} = 2.26Kohm * 1.93139mA = 4364.9414mv \approx 4.364v
$$
差分电压(正输出对负输出)的绝对值为:
$$
v_{out} * 2=4364.9414mv * 2=8729.8828mv \approx 8.729V
$$
第四步:计算IV转换电路的反馈电容(C1,C6)
为补偿放大器反相输入的寄生电容,必须为反馈电跨接电容。 该电容还可限制放大器或 DAC 的高频噪声量,它可能通过其他电路混叠到音频范围。
反相输入端的电容未知,因此电容值应在不引起音信号显著相移的条件下尽可能大些。 该电路的设计目标是相移小于 -5°。 为此,假定互阻抗放大器和差动放大器级形成同等相移,20kHz 下的互阻抗放大器相移应设为 -2.5°。 确定 20kHz 时的相移后,即可计算极点频率:
$$
\theta=-tan^{-1}\bigg(\frac{f}{f_p}\bigg)\rightarrow f_p \
$$
$$
f_p=\frac{f}{tan(-\theta)}=\frac{20000Hz}{tan(-2.5°)}\approx 458075 Hz
$$
使用极点频率和反馈电阻值可计算最大反馈电容:
$$
C_f ≤ \frac{1}{2\pi * R_{fb} * f_p}≤ \frac{1}{2\pi * 2.26Kohm * 458075 Hz} \approx 1.537*10^{-10}F=153.7pF
$$
即最大反馈电容应小于153.7pF。
选择小于这个数的最大的买得到的电容就行了。
在这个设计里面选择100pF。
第五步:计算偏置电压Vbias
DAC 输出代码为 0 时仍会存在输出电流,原因是DAC 存在偏移。 VBias 电压施加在互阻抗放大器的同相输入端(IN+),确保 DAC 代码为 0 时将输出稳定在 0V。
偏置电压Vbias的计算方法为
$$
V_{out} = 0V = V_{bias} * \bigg( 1+ \frac{R_{fb}}{R_{dac}}\bigg) - \bigg(\frac{AVCC}{2}\bigg) * \bigg( 1+ \frac{R_{fb}}{R_{dac}}\bigg)
$$
即
$$
V_{bias}=\frac{\bigg(\frac{AVCC}{2}\bigg) * \bigg(\frac{R_{fb}}{R_{dac}}\bigg)}{\bigg( 1+ \frac{R_{fb}}{R_{dac}}\bigg)}
$$
代入数值
$$
V_{bias}=\frac{\bigg(\frac{3.3V}{2}\bigg) * \bigg(\frac{2.26Kohm}{774_{ohm}}\bigg)}{\bigg( 1+ \frac{2.26Kohm}{774_{ohm}}\bigg)} \approx 1.22907V
$$
给计算器复制黏贴用的:((3.3/2)*(2260/774))/(1+(2260/774))
然后选择分压比例最接近的电阻分得这个电压就行了。
在这个设计里面选择从AVCC(3.3v)分压,上臂10.7Kohm,下臂6.34Ohm,分得电压大约1.228V。
至此,IV转换电路设计完成。
第六步:计算耳放的电压衰减系数
差分放大器可实现的衰减量取决于所需的最大输出电压水平。 便携式应用所用的耳机通常为低阻抗(16ohm或 32ohm),因此无需高电压来发出响亮声音。 例如,要向 32ohm 耳机提供 10mW 功率,输出电压只需0.566Vrms。
这种输出水平表明,差分放大器的衰减量应足够大才能获得最佳系统整体噪声性能。 但耳机输出也常用于将便携式电子产品连接到大型音频系统(通过模拟辅助输入)。 因此,采用典型的 line level 电平(+4dBu,1.228Vrms)作为最大输出电压。 差分放大器衰减量的计算方法是:输出幅值除以差分输入幅值。
由第三步可得:
IV转换输出的差分电压(正输出对负输出)的绝对值为:
$$
v_{out} * 2=4364.9414mv * 2=8729.8828mv \approx 8.729V
$$
转换成有效值:
$$
v_{outrms}= \frac{v_{out}}{\sqrt{2}} = \frac{8.729}{1.414}=6.17326V_{rms}
$$
采用典型的 line level 电平(+4dBu,1.228Vrms)作为最大输出电压,电压衰减系数的计算方法为:
$$
A=\frac{v_{out}}{v_{in}} = \frac{1.228Vrms}{6.17326Vrms}=0.19892
$$
第七步:计算耳机放大器的反馈电阻(R5,R7,R2,R11)
第六步的衰减系数决定了差分放大器中所用电阻值之比:
$$
A=\frac{R_2}{R_5}=\frac{R_{11}}{R_7}
$$
上述电阻值应足够低,避免引入明显的热噪声,同时也应足够高,避免互阻抗放大器输出负载过大。 根据TI手册,R5 和 R7 的值为 1.6Kohm 时可获得最佳性能。 此时可计算出 R2 和 R11:
$$
R_2=R_{11}=A *1.6K_{ohm}=0.19892*1.6K_{ohm}=0.318272K_{ohm} \approx 318_{ohm}
$$
选择阻值最接近的买得到的就行了。
在这个设计里面R2,R11选择316ohm电阻,R5,R7选择1.6Kohm电阻。
第八步:计算耳机放大器的反馈电容(C8,C2)
这些电容也可用于辅助维持特定条件下的电路稳定性。 如互阻抗放大器部分所述,上述电容值受限于各自在音频范围内形成的相移。 电容 C2 和 C8 生成的极点频率为:
$$
F_p = \frac{1}{2 \pi * (R_2 或R_{11}) * (C_2或C_8)}
$$
其中,Fp是第四步算出来的极点频率。
即
$$
C_2=C_8 ≤ \frac{1}{2 \pi *(R_2 或R_{11})* F_p}=\frac{1}{2 \pi *(316_{ohm})* 458075 Hz}=1.099503*10^{-9}F=1099pF
$$
给计算器复制黏贴用的:((1)/(2*3.14159265358*316*458075))
选择小于这个数的最大的买得到的电容就行了。
这个设计里面选择820pF。
第九步:计算运放并联输出的均流电阻(R6,R8)
电阻 R6 和 R8 可以平衡放大器 U2A 和 U2B 分担的负载电流。 由于放大器开环增益间存在差异,上述电阻可防止放大器之间出现电流反向驱动。 另外,上述电阻还能够降低两个输出电路间循环的直流电流,该电流是由于两个器件不同的输入失调电压导致的。 差动放大器的反馈环路在负载平衡电阻后闭合以保持低闭环输出阻抗。
两个输出电路中的直流循环电流计算公式如下:
$$
i_{dc}=\frac{V_{os(U2B)}}{R_6 + R_8}
$$
音频运算放大器的偏移电压通常是没有修整(trim)过的,因此对于 U2B 可选的运算放大器,其偏移电压最高可能达到 2mV。限制整体电路的静态功耗,直流循环电流需限定为 100μA。 R6 和 R8 的值为:
$$
R_6 + R_8=\frac{V_{os(U2B)}}{i_{dc}}=\frac{2mV}{100uA}=20_{ohm}
$$
选择 10ohm 作为这两个电阻的阻值,确保负载电流在两个放大器间平均分配。
这个设计里面选取R6=R8=10ohm。
第十步:可选,R10和C9的给出
根据ti手册:
某些运算放大器可能还需要 R10 和 C9 来确保稳定性。 要理解其功能,可考虑放大器 U2B 同时具有正负反馈。 正反馈由 U2A 向 U2B 的同相输入施加。 R10 和 C9 组成的低通滤波器可降低 U2B 的正反馈,提升稳定性。 不过,这同时也会降低 U2B 对总输出负载电流的贡献,导致失真程度增大。 在该设计中,20kHz 时允许并行放大器的贡献降低 0.01dB。
R10 = 249Ω,C9 = 1.8nF 时,截止频率稍有下降 (355kHz),但这对音频的影响非常小。
附加:元件选择
电阻
互阻抗放大器中的反馈电阻(R1,R9)以及差分放大器的各个构成电阻(R2、R5、R7、R11)应采用高精度(0.1%) 电阻,以便实现最佳性能。 选择高精度电阻可确保互阻抗放大器的输出电压良好匹配。 高精度电阻还能够提高差分放大器的共模抑制特性,降低耳机输出的直流偏移,甚至能够消除互阻抗放大器或 DAC的谐波失真。
电容
所有信号通路上的电容(C1、C2、C6、C8、C9)必须都是 C0G/NP0 类型陶瓷电容。 其它类型的陶瓷电容(X7R、X5R 等)会导致大量失真并降低电路性能。
运放输入的说明
由于所有的运放都存在负反馈,因此,正常情况下,运放的同相输入和反相输入电压会相等,因此,可以不选择输入轨到轨的运放。
参考
手把手算电流输出型DAC的IV转换电路原件参数计算及耳机放大器原件参数(参考TI,以ES9038q2m为例)