运放易用速通篇！几分钟教会你运放基本用法

运放，全名运算放大器（OPAMP），堪称模电芯片当中的一大难关。但大部分情形我们在面临要求不高的运放电路读图或设计时，运用一些技巧可以帮助我们更轻松地使用运放。

本文主要基于理想运算放大器进行讨论，仅作为快速计算和快速理解的帮助。对于要求较高的场合，请结合运放原理和实际运放参数进行设计。

理想运放的基本结构

一个理想运放的符号通常如下所示：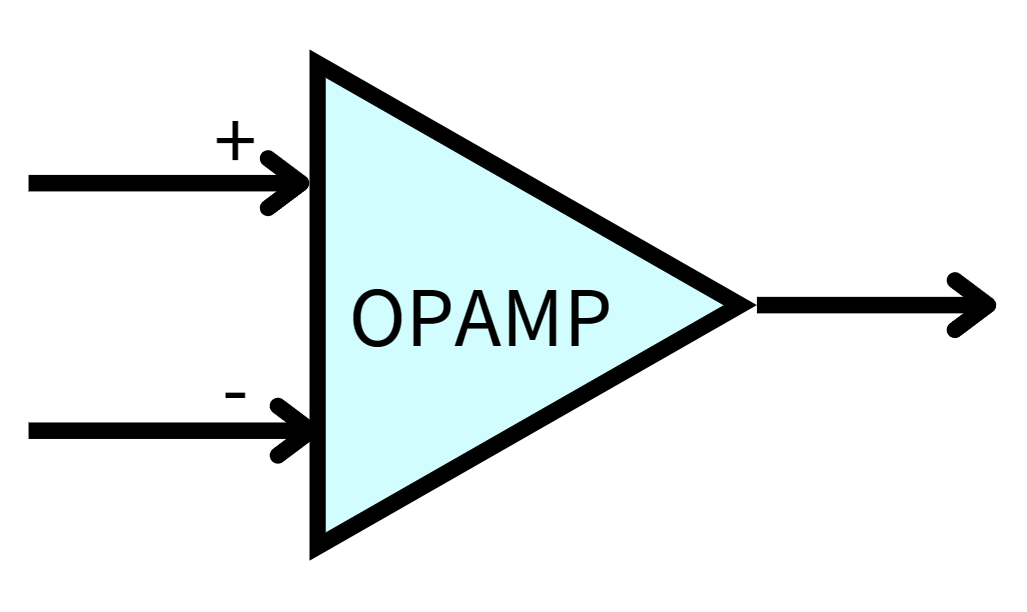

其具有两个输入端（分别标记有+、-）和一个输出端（运放的供电此处忽略）。
同时，对于理想运放，其两个输入端的输入电阻无穷大、等效电容为0，其输出阻抗为0。
不要被以上内容吓到，我们马上就揭秘它的工作逻辑。

理想运放的逻辑

本文中我们不去深究运放的内部结构和核心原理。我们只在此给出两条结论：

• 理想运放会通过调节输出端的电压，尽全力使得两个输入端的电压相等。
• 理想运放会将输入端+的电压与输入端-的电压之差，乘以一个极大的倍数（可以想象是$1\times10^{12}$那么大）输出到输出端。

这两条结论此处不证，有兴趣的同学可以自行研究。熟记这两条结论有助于我们快速理解和计算理想运算放大器电路。

小试牛刀

我们现在用它来分析常见的几种运放放大电路作为练习。

同相放大电路

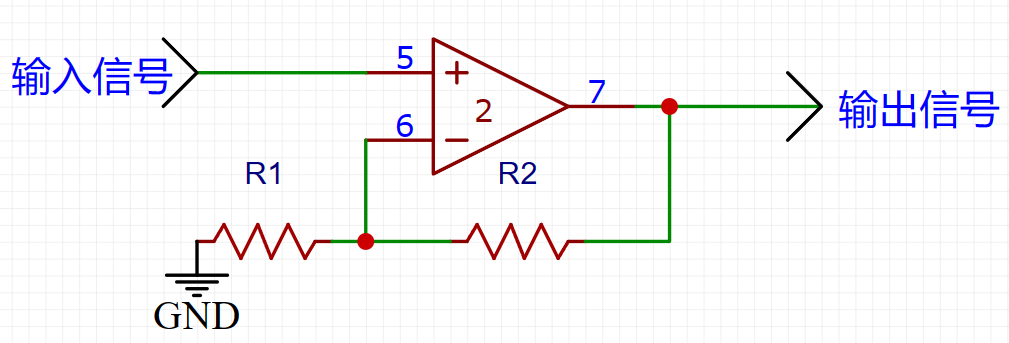
看到这个图，一些同学要开始头痛了。不要急，我们用刚刚的结论1分析。
运放会调节输出端的电压，使得两个输入端的电压相等，则可以列出这个表达式：
$$
U_{in}=(\frac{R_{1}}{R_{1}+R_{2}})\times U_{out}
$$
等号左边是运放输入+的电压，等号右边是运放输入-的电压。

适当变形就得到了教科书的经典公式：
$$
U_{out}=(\frac{R_{1}+R_{2}}{R_{1}})\times U_{in}
$$

当R1开路，R2短路时，电路变为下图（单位增益同相放大，即跟随器电路）：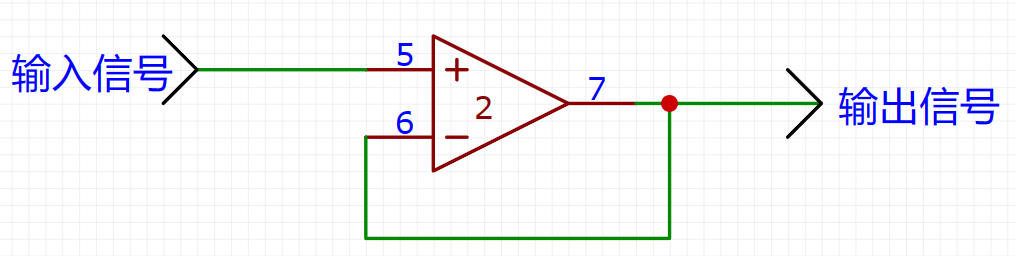

等式也变形如下：
$$
\begin{align}
U_{out} & = (\frac{R_{1}}{R_{1}}+\frac{R_{2}}{R_{1}})\times U_{in} \newline
& = (1+\frac{R_{2}}{R_{1}})\times U_{in} \newline
& = 1\times U_{in} \newline
& = U_{in}
\end{align}
$$

反相放大电路

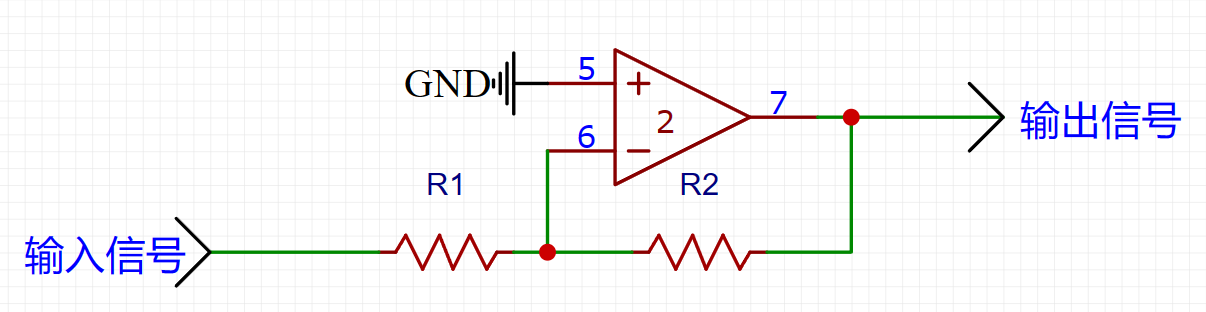
仍然用结论1分析。列出这个表达式：
$$
0=(\frac{R_{1}}{R_{1}+R_{2}})\times(U_{out}-U_{in})+U_{in}
$$
等号左边是运放输入+的电压（由于接地，等于0），等号右边是运放输入-的电压。

对等式进行一些变形。先分离变量把Uin和Uout拿到等式两边。
$$
(\frac{R_{1}}{R_{1}+R_{2}})\times U_{out}=-U_{in}+(\frac{R_{1}}{R_{1}+R_{2}})\times U_{in}
$$
然后合并同类项。
$$
(\frac{R_{1}}{R_{1}+R_{2}})\times U_{out}=(\frac{R_{1}-R_{1}-R_{2}}{R_{1}+R_{2}})\times U_{in}
$$
将系数移项到右侧，然后整理。
$$
U_{out}=-(\frac{R_{2}}{R_{1}})\times U_{in}
$$
嗯，又是一个教科书的经典公式。

总结

灵活运用给出的两条结论，对于计算和理解理想运放电路有较好的帮助。
结论1其实就是模电书所说的“虚短”，只是用更通俗的方式来讲。